Answer:
The required time is 3.54 seconds approximately or
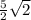 seconds.
seconds.
Explanation:
Consider the provided function.
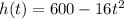
Where t represents the time in seconds and h represents the height.
It is given that we need to find the time to reach a height of 400 feet.
Substitute h(t)=400 in the above function.
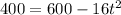

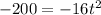
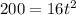
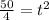
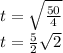
Neglect the negative value as time should be a positive number.
Or

Hence, the required time is 3.54 seconds approximately.