Question

An object dropped from a height of 600 feet has a height, h(t), in feet after t seconds have elapsed, such that h(t) = 600 − 16t 2 . Express t as a function of height h, and find the time to reach a height of 400 feet.

Answer 1

given h = 600 - 16t ( add 16t to both sides )

16t + h = 600 ( subtract h from both sides )

16t = 600 - h ( divide both sides by 16 )

t =
`(600-h)/(16)`

when h = 400

t =
`(600-400)/(16)` =
`(200)/(16)` = 12.5 seconds

Answer 2

The required time is 3.54 seconds approximately or
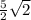`(5)/(2)√(2)` seconds.

Explanation:

Consider the provided function.

`h(t) = 600-16t^2`

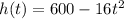
Where t represents the time in seconds and h represents the height.

It is given that we need to find the time to reach a height of 400 feet.

Substitute h(t)=400 in the above function.

`400= 600-16t^2`

`400- 600=-16t^2`

`-200=-16t^2`

`200=16t^2`

`(50)/(4)=t^2`

`t=\sqrt{(50)/(4)} \\t=(5)/(2)√(2)`

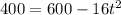
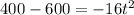
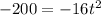
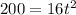
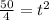
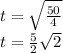
Neglect the negative value as time should be a positive number.

Or

`t\approx 3.54`

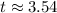
Hence, the required time is 3.54 seconds approximately.