Answer:
A
Explanation:
We are given a right triangle with a base of x feet and a height of h feet, where x is constant and h changes with respect to time t.
The angle in radians is defined by:
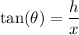
And we want to find the relationship that describes dθ/dt and dh/dt.
So, we will differentiate both sides with respect to t where x is a constant:
![\displaystyle (d)/(dt)[\tan(\theta)]=(d)/(dt)\Big[(h)/(x)\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/5yxzshzr2sy907bacgyoa5bbzit9mlpgrh.png)
Differentiate. Apply the chain rule on the left. Again, remember that x is just a constant, so we can move it outside the derivative operator. Therefore:

Since we know that tan(θ)=h/x, h is the opposite side of our triangle and x is the adjacent. Therefore, by the Pythagorean Theorem, our hypotenuse will be:
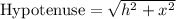
Since secant is the ratio of the hypotenuse to adjacent:
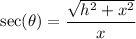
So:
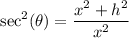
By substitution, we have:
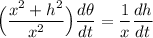
By multiplying both sides by the reciprocal of the term on the left:
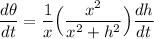
Therefore:
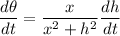
Our answer is A.