Question

Need help #3. The answer is shown, but I don’t know how to get to the answer. Please teach and show steps.

Answer 1

A

Explanation:

We are given a right triangle with a base of x feet and a height of h feet, where x is constant and h changes with respect to time t.

The angle in radians is defined by:

`\displaystyle \tan(\theta)=(h)/(x)`

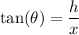
And we want to find the relationship that describes dθ/dt and dh/dt.

So, we will differentiate both sides with respect to t where x is a constant:

`\displaystyle (d)/(dt)[\tan(\theta)]=(d)/(dt)\Big[(h)/(x)\Big]`

Differentiate. Apply the chain rule on the left. Again, remember that x is just a constant, so we can move it outside the derivative operator. Therefore:

`\displaystyle \sec^2(\theta)(d\theta)/(dt)=(1)/(x)(dh)/(dt)`

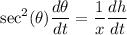
Since we know that tan(θ)=h/x, h is the opposite side of our triangle and x is the adjacent. Therefore, by the Pythagorean Theorem, our hypotenuse will be:

`\text{Hypotenuse}=√(h^2+x^2)`

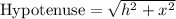
Since secant is the ratio of the hypotenuse to adjacent:

`\displaystyle \sec(\theta)=(√(h^2+x^2))/(x)`

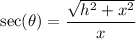
So:

`\displaystyle \sec^2(\theta)=(x^2+h^2)/(x^2)`

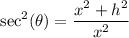
By substitution, we have:

`\displaystyle \Big((x^2+h^2)/(x^2)\Big)(d\theta)/(dt)=(1)/(x)(dh)/(dt)`

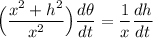
By multiplying both sides by the reciprocal of the term on the left:

`\displaystyle (d\theta)/(dt)=(1)/(x)\Big((x^2)/(x^2+h^2)\Big)(dh)/(dt)`

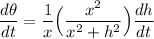
Therefore:

`\displaystyle (d\theta)/(dt)=(x)/(x^2+h^2)(dh)/(dt)`

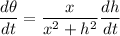
Our answer is A.