Question

Need help #1. The answer is shown, but I don’t know how to get to the answer. Please teach and show steps.

Answer 1

Let x and y be functions of time t such that the sum of x and y is constant.

(B) is the right answer

Answer 2

B

Explanation:

We are given that x and y are functions of time t such that x and y is a constant. So, we can write the following equation:

`x(t)+y(t)=k,\text{ where $k$ is some constant}`

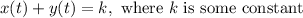
The rate of change of x and the rate of change of y with respect to time t is simply dx/dt and dy/dt, respectively. So, we will differentiate both sides with respect to t:

`\displaystyle (d)/(dt)\Big[x(t)+y(t)\Big]=(d)/(dt)[k]`

Remember that the derivative of a constant is always 0. Therefore:

`\displaystyle (dx)/(dt)+(dy)/(dt)=0`

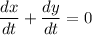
And by subtracting dy/dt from both sides, we acquire:

`\displaystyle (dx)/(dt)=-(dy)/(dt)`

Hence, our answer is B.