Answer:
B
Explanation:
We are given that x and y are functions of time t such that x and y is a constant. So, we can write the following equation:
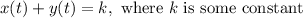
The rate of change of x and the rate of change of y with respect to time t is simply dx/dt and dy/dt, respectively. So, we will differentiate both sides with respect to t:
![\displaystyle (d)/(dt)\Big[x(t)+y(t)\Big]=(d)/(dt)[k]](https://img.qammunity.org/2022/formulas/mathematics/college/ic5my31y69eo6f2upj0e4l6j35tkg9t83j.png)
Remember that the derivative of a constant is always 0. Therefore:
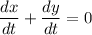
And by subtracting dy/dt from both sides, we acquire:
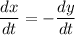
Hence, our answer is B.