Question

A circle is centered at C(−1,−3) and has a radius of 6.Where does the point P(-6,-6) lie?

Answer 1

inside the circle

Step-by-step explanation:

Khan academy confirmed

Answer 2

The equation of circle is

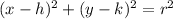`(x-h)^(2)  + (y-k)^(2) = r^(2)`. -------- (h, k) is the center of the circle.

The point is inside the circle if the distance from it to the centre is less than the radius. Symbolically, this is

`\sqrt{({x - h})^(2) +{(y - k)}^(2)} < r`

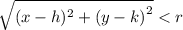
and point is outside the circle if the distance from it to the centre is great than the radius. Symbolically, this is

`\sqrt{({x - h})^(2) +{(y - k)}^(2)} > r`

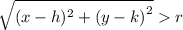
and if this distance is equal to r then it lies on the cirlce.Symbolically, this is

`\sqrt{({x - h})^(2) +{(y - k)}^(2)} = r`

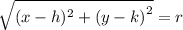
now by putting the value of (x , y) and (h,k)

`\sqrt{(-6 - -1)^(2) + (-6 - -3)^(2)}`

`=√(25 + 9)`

`=√(34)`

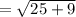
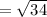
since our r is 6 and

=5.8 < 6

So the point (-6 , -6) is inside the circle.