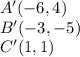Answer:
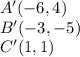
Explanation:
The given vertices are

Now, when we reflect a figure across the x-axis, the coordinates of that figure change. In this case, all vertical coordinates (y-variable) must change to its opposite in order to ensure the reflection across the x-axis.
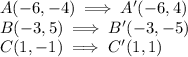
Therefore, the vertices of the reflected image are