Question

What is the solution set of the equation using the quadratic formula?

x2+6x+10=0



{−3+i, −3−i}


{−3+2i, −3−2i}


{−6+2i, −6−2i}


{−2i, −4i}



Jamal solved the equation by completing the square.


x2−8x+14=0




Which equation shows one of the steps Jamal could have taken to complete the square?





x2−8x+16=−14+16


x2−8x+64=−14+64


x2−8x+16=−14


x2−8x+64=−14

Answer 1

(1)

we are given

`x^2+6x+10=0`

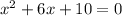
we can use quadratic formula

`\mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:}`

`x=(-b\pm √(b^2-4ac))/(2a)`

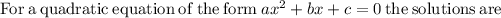
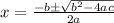
now, we can compare and find a , b and c

we get

`a=1,b=6,c=10`

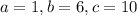
now, we can plug these values into quadratic formula

`x=(-6\pm √(6^2-4(1)(10)))/(2(1))`

`x=(-6+√(6^2-4\cdot \:1\cdot \:10))/(2\cdot \:1)`

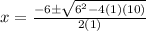
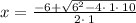
we can simplify it

`x=-3+i`

`x=(-6-√(6^2-4\cdot \:1\cdot \:10))/(2\cdot \:1)`

`x=-3-i`

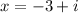
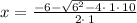
so, we will get solution

{−3+i, −3−i}.........Answer

(2)

we are given equation as

`x^2-8x+14=0`

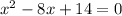
Since, Jamal solve this equation by completing square

so, firstly we will move constant term on right side

so, subtract both sides by 14

`x^2-8x+14-14=0-14`

`x^2-8x=-14`

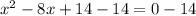
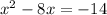
we can write

`-8x=-2* 4* x`

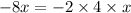
so, we will add both sides by 4^2

`x^2-8x+4^2=-14+4^2`

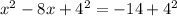
we get

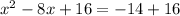`x^2-8x+16=-14+16`..............Answer