(1)
we are given
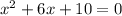
we can use quadratic formula
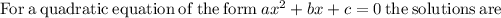

now, we can compare and find a , b and c
we get
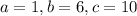
now, we can plug these values into quadratic formula
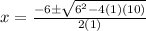
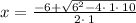
we can simplify it
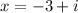
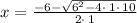

so, we will get solution
{−3+i, −3−i}.........Answer
(2)
we are given equation as
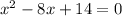
Since, Jamal solve this equation by completing square
so, firstly we will move constant term on right side
so, subtract both sides by 14
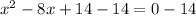
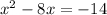
we can write
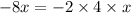
so, we will add both sides by 4^2
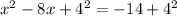
we get
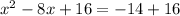 ..............Answer
..............Answer