Given
The equation is in the form
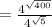
Simplify the above equation
To proof
As given in the question the equation is written in the form
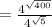
By using the exponent property
when you divide powers with the same base you just have to subtract the exponents. i.e
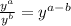
y is not equal to zero.
Now apply this property to the above equation
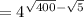
As
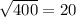
now put this in the above equation
we get
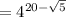
Hence proved