hello!
In order to find the reciprocal of a number, we should flop it over.
Now, "flopping over" is not the same as "changing the sign"
If we have a fraction, and we're asked to find its reciprocal, then the numerator and denominator switch places.
Please consult the following formula for more details:-
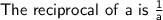

According to the
 , the reciprocal of
, the reciprocal of
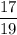 is:-
is:-
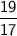
note:-
Hope everything is clear; if you need any explanation/clarification, kindly let me know, and I'll comment and/or edit my answer :)