We know that
triangles ADE and ABC are similar triangles
so, the ratios of their sides must be same
now, we will find value of sides
we are given
AD=12
DB=6
AE=14
EC=7
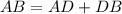
now, we can plug values
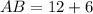
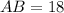
so, we can get ratio
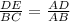
now, we can plug values
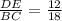
So, the ratio in simplest form is
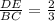 ..............Answer
..............Answer