Let the initial mass be represented by
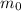 . Therefore,
. Therefore,
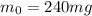 .
.
Let the final mass (or present mass be represented by
 . Therefore,
. Therefore,
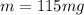 .
.
Now, we are given that the rate of decay is 8% or 0.008 per day. Therefore, the amount of substance remaining after each day will be
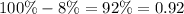 . Let us represent this by
. Let us represent this by
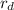 .
.
Please note that the equation guiding such decays is always given by:
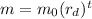 , where t is the time.
, where t is the time.
Thus, the above equation will give in our case:
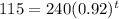
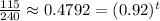
Taking natural logarithm on both sides we get:
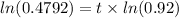
Therefore,

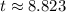 days<9 days
days<9 days
Thus, in 9 days there will be further decay and the sample left will definitely be less than 115 milligrams.
The only option which matches this reality is Option C. Therefore, Option C is the correct answer.