Answer
a = 3.674 m / s ^ 2
t = 3.13 s
Using the kinematic equations for the movement we have:
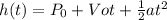 (1)
(1)
 (2)
(2)
Where:
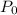 = initial position
= initial position
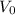 = initial velocity
= initial velocity
a = acceleration
t = time in seconds
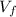 = final speed
= final speed
We know:
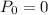

h = 18 m

So:
From (2) we have that:

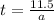
From (1) we have to:
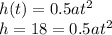
Then we clear "a" to find the acceleration.
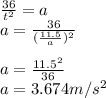
Then, the time it takes to reach this speed is:
