Question

Explain why the solution of 5x – 3 > 14.5 or 2x+5/3 < 4 has a solution of all real numbers, with one exception.

Answer 1

When solving the first inequality, you get x > 3.5. When solving the second inequality, you get x < 3.5. The solution of an “or” compound in equality is everything in both solution sets, so the solution set is all of the numbers less than 3.5 and greater than 3.5. Since neither of the inequalities includes 3.5, the compound inequality has a solution of all real numbers except 3.5.

Step-by-step explanation:

Answer 2

Answer: The solution of given inequalities is all real number except [1.167, 3.5].

Step-by-step explanation:

The given inequalities are

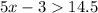`5x-3>14.5` ....(1)

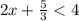`2x+(5)/(3)<4` .... (2)

Solve first inequality.

`5x-3>14.5`

`5x>14.5+3`

`x>(17.5)/(5)`

`x>3.5`

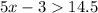
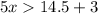
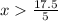
Solve second inequality.

`2x+(5)/(3)<4`

`2x<4-(5)/(3)`

`2x<(12-5)/(3)`

`x<(7)/(6)`

`x<1.167`

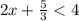
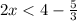
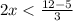
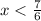
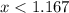
The solution of first or second inequality is all real number less than 1.167 and all rea number more than 3.5. It means the combined solution of both inequalities is all real number except [1.167, 3.5].