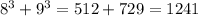Question

Find two consecutive numbers that cubes add up to 1,241

Answer 1

If the first of the two integers is
`x`, the next one is
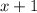`x+1`. So, the sum of their cubes are

`x^3+(x+1)^3 = x^3+x^3 + 3 x^2 + 3 x + 1 = 2x^3+3x^2+3x+1`

So, we have the following equation:

`2x^3+3x^2+3x+1 =1241 \iff 2x^3+3x^2+3x-1240 =0`

By the rational root theorem, if this polynomial admits a rational root, it is a fraction
`(p)/(q)` where p divides 1240 and q divides 2 (i.e., q=1 or q=2). You'll have to go with a bit of trial and error here, because the standard formula for solving cubic equation is quite complicated.

Eventually, you'll arrive to p=8, q=1, and if you plug 8 into the equation you'll see that it is a solution. So, the two numbers are 8 and 9, in fact

`8^3+9^3=512+729=1241`