Question

Explain why P(A|D) and P(D|A) from the table below are not equal.

Answer 1

Sample Response: The two conditional probabilities are not equal because each has different given events. P(A|D) has event D as its given event, resulting in 2/10 for a probability. P(D|A) has event A as its given event, resulting in 2/8 for a probability.

Answer 2

The Probability that Event A and Event D occur is equal to the probability Event A occurs times the probability that Event D occurs, given that A has occurred.

`P(A\cap D)=P(A)\cdot P(D/A)`

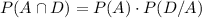
We can find the values of
`P(A/D)` and
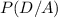`P(D/A)` using the above form formula.

`P(D/A)=(P(A\cap D))/(P(A))` ;

`P(A/D)=(P(D\cap A))/(P(D))`

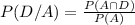From the given table, we have the values of P(A), P(D),
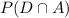`P(D\cap A)` and
`P(A\cap D)`.

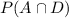Since, Probability=
`(The number of wanted outcomes )/(the number of possible outcomes)`

∴
`P(A)=(8)/(17)`,
`P(D)=(10)/(17)`,
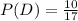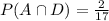`P(A\cap D)=(2)/(17)` and
`P(D\cap A)=(2)/(17)`

Now, putting these values in above formula we get,

`P(D/A)=\frac{(2)/(17)} {(8)/(17)}`

`P(D/A)=\frac{2} {8}=(1)/(4)`

`P(D/A)= (1)/(4)`.

`P(A/D)=\frac{(2)/(17)} {(10)/(17)}=(2)/(10)`

`P(A/D)=(1)/(5)`

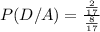
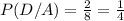
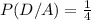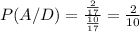
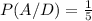
As, you can see above that the values of P(A|D) and P(D|A) are not equal.