Answer:
Option C). (10, 7.5)
Explanation:
We have to find the coordinates of point M that divides the segment AB into a ratio of 5:5.
Vertices A and B are (0, 15) and (20, 0)
Ratio 5:5 is simply the ratio 1:1 means point M is the midpoint of segment AB.
So x-coordinate of M will be
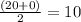
and y - coordinate will be =

Therefore Option C. (10, 7.5) are the coordinates of point M.