Question

Find the point, M, that divides segment AB into a ratio of 5:5 if A is at (0, 15) and B is at (20, 0).

A) (35, 10)
B) (20, 10)
C) (10, 7.5)
D) (17.5, 5)

Answer 1

C

a ratio of 5 : 5 simplifies to 1 : 1, which basically means we require the midpoint of the line segment

using the midpoint formula

M = [
`(1)/(2)` (0 + 20 ),
`(1)/(2)` (15 + 0)] = (10, 7.5 )

Answer 2

Option C). (10, 7.5)

Explanation:

We have to find the coordinates of point M that divides the segment AB into a ratio of 5:5.

Vertices A and B are (0, 15) and (20, 0)

Ratio 5:5 is simply the ratio 1:1 means point M is the midpoint of segment AB.

So x-coordinate of M will be
`((20+0))/(2)=10`

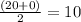
and y - coordinate will be =
`((15+0))/(2)=7.5`

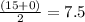
Therefore Option C. (10, 7.5) are the coordinates of point M.