Answer:
a) The slope is : 3.333
b)
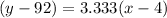
c)

Explanation:
a) - The formula to calculate the slope is:

- Use the given points to calculate the slope:
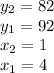
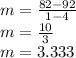
b) - The equation of the linear model in point-slope form is:

Where
 is the slope and
is the slope and
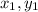 are the coordinates of a point.
are the coordinates of a point.
- Substitute values:
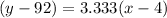
c) - The equation of the linear model in slope-intercept form is:

Where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.
- Let's find
 . Use one of the points given in the problem to solve for
. Use one of the points given in the problem to solve for
 :
:

- Therefore, the equation is:
