Question

Find the slope of the tangent line to the graph of f at the given point. f(x) = x√ at (36,6) 1/3 1/12 3 12

Answer 1

`slope = (1)/(12)`

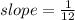
Explanation:

Here is another method to solve your problem. I am showing this method because this is the first method normally taught and a student might not of had the chance yet to learn the other methods

We can solve this problem by using limits and the following function

`\lim_(h\to 0) (f(x+h) - x)/(h)`

`\lim_(h\to 0) (√(x+h) - √(x))/(h)`

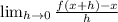
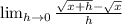
Next multiply by the conjugate of the numerator.

`\lim_(h\to 0) (√(x+h) - √(x))/(h) * (√(x+h) + √(x))/(√(x+h) + √(x))`

`\lim_(h\to 0) (x + h - x)/(h(√(x+h) + √(x)))`

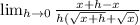
Cancel the x - x

`\lim_(h\to 0) (h)/(h(√(x+h) + √(x)))`

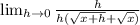
Divide out the h

`\lim_(h\to 0) (h)/(h(√(x+h) + √(x)))`

`\lim_(h\to 0) (1)/((√(x+h) + √(x)))`

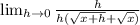
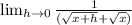
Plugin 0 where h is located

`\lim_(h\to 0) (1)/((√(x+h) + √(x)))`

`\lim_(h\to 0) (1)/((√(x+0) + √(x)))`

`\lim_(h\to 0) (1)/((√(x) + √(x)))`

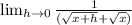
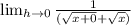
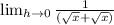
Combine Like terms in denominator

`\lim_(h\to 0) (1)/((√(x) + √(x)))`

`\lim_(h\to 0) (1)/(2√(x))`

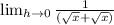
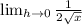
Now lets use our derivative and plugin 36 where x is located and solve

`(1)/(2√(x))`

`(1)/(2√(36))`

`(1)/(2(6))`

`(1)/(12)`

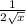
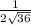
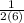
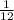
Note, this is a harder method but it is normally the first method taught in Calculus 1.

Answer 2

slope =
`(1)/(12)`

the slope is the value of f' (36)

f(x) = √x =
`x^{(1)/(2) }`

f'(x) =
`(1)/(2)`
`x^{-(1)/(2) }` =
`(1)/(2√(x) )`

f'(36) =
`(1)/(2(6))` =
`(1)/(12)`