Answer
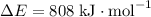
Step-by-step explanation
Forming chemical bonds releases energy whereas breaking them requires an input of energy.
Typical chemical reaction involves breaking preexisting bonds and forming new ones. The amount of energy absorbed in the first process is not necessarily equal to the energy released in the second. Depending on the relationship between the two energies, their difference is either released or absorbed in the chemical reaction.
Start by identifying bonds broken and formed in this chemical process:
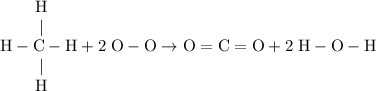
Bonds Broken per reaction:
- Four carbon-hydrogen single bonds
 as in one methane
as in one methane
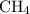 molecule;
molecule; - Two oxygen-oxygen bonds
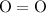 as in two oxygen
as in two oxygen
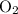 molecules with one bond in each molecule.
molecules with one bond in each molecule.
Bonds Formed per reaction:
- Two carbon-oxygen double bonds
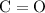 as in one carbon dioxide
as in one carbon dioxide
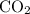 molecule.
molecule. - Four hydrogen-oxygen single bonds
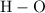 as in two water
as in two water
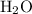 molecules.
molecules.
![\text{Energy Change} = \text{Energy Released} - \text{Energy Absorbed}\\\phantom{\text{Energy Change}} = E[\text{Bonds Formed}] - E[\text{Bonds Broken}]](https://img.qammunity.org/2019/formulas/chemistry/college/rvv8ty656he1wsv31suz0n409fydirfqyw.png)
Referring to a thermodynamic data table of bond energies,
Note that due to the conservation of energy, the energy required to break a chemical bond shall be the same as the energy released on its formation.
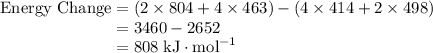
3460 kJ, the energy released in the formation of bonds is greater than 2652 kJ, the energy absorbed to break bonds in the reactant. The energy change is thus positive and 808 kJ of energy is released per mole reaction.