The correct answer is option B.
Let the basic calendars be = x
Let the deluxe calendars be = y
Total calendars are = 72 , so equation becomes:
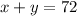 .............(1)
.............(1)
Cost of 1 basic calendar = $10
So, cost of all basic calendars will be = 10x
Cost if 1 deluxe calendar = $15
So, cost of all deluxe calendars = 15y
As given, the number of deluxe calendars must be greater than or equal to 3 times the number of basic calendars, the equation becomes
y=3x ...............(2)
Putting the value of y from (2) in (1)
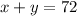
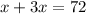
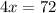
x=18
As, y=3x
y=
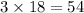
So we have 18 basic calendars and 54 deluxe calendars.
Cost of 18 basic calendars will be=
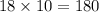
Cost of 54 deluxe calendars will be =
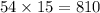
So total amount is = $990
Hence, the maximum revenue is $990.