Question

Jerrica is selling calendars to raise money for a community group she belongs to. A basic calendar sells for $10 and a deluxe calendar sells for $15. The number of deluxe calendars Jerrica sells must be greater than or equal to 3 times the number of basic calendars she sells. She has at most 72 calendars to sell. The number of basic calendars sold is represented by x and the number of deluxe calendars sold is represented by y. What is the maximum revenue she can make?

A. $810
B. $990
C. $1080
D. $1296

Answer 1

The CORRECT answer is $1080

Explanation:

Your answer would be choice C

Answer 2

The correct answer is option B.

Let the basic calendars be = x

Let the deluxe calendars be = y

Total calendars are = 72 , so equation becomes:

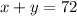`x+y=72` .............(1)

Cost of 1 basic calendar = $10

So, cost of all basic calendars will be = 10x

Cost if 1 deluxe calendar = $15

So, cost of all deluxe calendars = 15y

As given, the number of deluxe calendars must be greater than or equal to 3 times the number of basic calendars, the equation becomes

y=3x ...............(2)

Putting the value of y from (2) in (1)

`x+y=72`

`x+3x=72`

`4x=72`

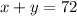
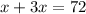
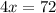
x=18

As, y=3x

y=
`3*18=54`

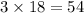
So we have 18 basic calendars and 54 deluxe calendars.

Cost of 18 basic calendars will be=
`18*10=180`

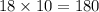
Cost of 54 deluxe calendars will be =
`54*15=810`

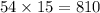
So total amount is = $990

Hence, the maximum revenue is $990.