For this case we have the following expression:
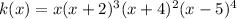
The roots are:
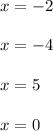
For example: For x = 0 we have
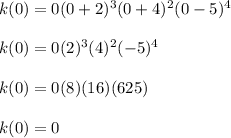
so it is shown that
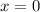 is a root.
is a root.
By definition, multiplicity represents the number of times a root is repeated in a polynomial, in turn it is given by the degree of the term that contains the root.
Thus:
The multiplicity of 0 is 1
The multiplicity of -2 is 3
The multiplicity of -4 is 2
The multiplicity of 5 is 4
Answer:
The multiplicity of 0 is 1
The multiplicity of -2 is 3
The multiplicity of -4 is 2
The multiplicity of 5 is 4