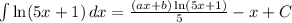Question

Ignore question number 10.(i) . Help me answer the number 10(ii) pleaseeeee.

Answer 1

Step-by-step explanation

The ii says "hence". This tells you that you must proceed from i above.

Given;

`y=(10x+2)\ln(5x+1)`

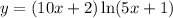
After differentiating in i, we had;

`(dy)/(dx)=10\ln(5x+1)+10`

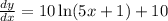
We now integrate both sides to obtain;

`\int\limits {(dy)/(dx)} \, dx =\int\limits {10\ln(5x+1)+10} \, dx`

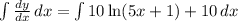
This gives,

`y =\int\limits {10\ln(5x+1)} \, dx+\int\limits {10} \, dx`

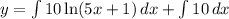
We now split the integral to obtain;

`y =\int\limits {10\ln(5x+1)} \, dx+\int\limits {10} \, dx`

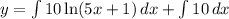
This implies that,

`y =\int\limits {10\ln(5x+1)} \, dx+10x +C`

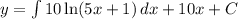
We rearrange to get,

`\int\limits {10\ln(5x+1)} \, dx = y-10x +C`

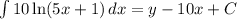
But

`y=(10x+2)\ln(5x+1)`

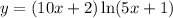
This implies,

10
`\int\limits {\ln(5x+1)} \, dx = (10x+2)\ln(5x+1)-10x +C`

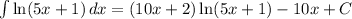
We divide through by 10.

`\int\limits {\ln(5x+1)} \, dx = 2((5x+1)\ln(5x+1))/(10)-x +(C)/(10)`

NB: The constant C divided by 10 is still a constant.

`\int\limits {\ln(5x+1)} \, dx = ((5x+1)\ln(5x+1))/(5)-x +C`

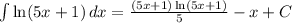
If a=5 and b=1 and we substitute, we get a general formula,but they were partially substituted to get.

`\int\limits {\ln(5x+1)} \, dx = ((ax+b)\ln(5x+1))/(5)-x +C`