The question is unclear regarding the boat's velocity. Is it 20 m/s south relative to the water, or relative to the earth? (It is a river, after all...)
There's also the possibility that the boat's velocity relative to the river is 0. Take the south direction to be negative and north to be positive, and denote by
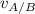 the velocity of a body A relative to a body B. Under these conditions,
the velocity of a body A relative to a body B. Under these conditions,

(B for boat, E for earth, W for water) so that the passenger's velocity relative to the earth is

(P for passenger)
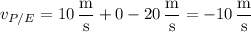
or 10 m/s south.