Question

Using the discriminant, determine the number of real solutions.

2x^2+7x-15=0

- no real solutions
-one real solution
-two real solutions

Answer 1

two real solutions

Explanation:

Answer 2

Since discriminant is positive, therefore, the given quadratic equation has two real solutions. Correct answer is the last option.

Explanation:

We have been given a quadratic equation and we need to figure out the number of real solutions of the equation.

`2x^(2)+7x-15=0`

We know that discriminant of a general quadratic equation
`ax^(2)+bx+c=0` is given by
`D=b^(2)-4ac`

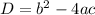
For the given quadratic equation
`2x^(2)+7x-15=0`, we have
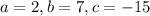`a=2,b=7,c=-15`. Upon substituting these values in the formula for discriminant, we get:

`D=7^(2)-4(2)(-15)`

`D=49+120`

`D=169`

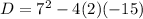
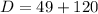
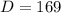
Since discriminant is a positive number, therefore, the given quadratic equation has two real solutions. Hence, the last option is the correct answer.