Step by Step Explanation
From the question,
the dimensions of the tank are;
L = 30 cm, way =0.075m and H = 15 cm
The density of water is given as
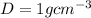
The unit of density given in the question means that the mass of the water is in grams and the volume should also be in
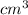
To find the volume of the water, we first convert the units of dimensions given in inches and metres to centimetres

This implies that ,

Also,
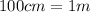
This implies that,

Now, the volume of water in the tank can hold, can be found from the relation;

This implies that,
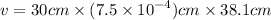
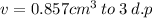
Finally, we can calculate the mass of the water from the relation given;

This in implies that
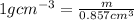
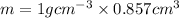

Hence the fish tank can hold 0.857g water.