Answer:
280 adult tickets, 40 student tickets and 80 children tickets were sold.
Explanation:
To solve this problem let's call:
x = number of tickets for adults
y = number of tickets for students
z = number of tickets for children
The income for the concert is $ 7840
Then we can raise the following equations according to the given conditions:
 (i)
(i)
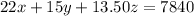 (ii)
(ii)
There are 40 more children in the concert than students:
So:
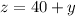 (iii)
(iii)
We then have 3 equations and 3 unknowns:
To solve the system we multiply the equation (i) by -22 and add it to the equation (ii)
So:
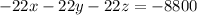
+

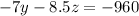 (iv)
(iv)
Now we multiply (iii) by 7 and add it to (iv)

+
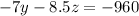
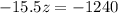
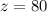 (v)
(v)
We substitute (v) in (iv) and we have
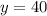 (vi)
(vi)
We substitute (v) and (vi) into (i) and we have:

280 adult tickets, 40 student tickets and 80 children tickets were sold.