Answer: B) The lengths of both transverse axes are the same.
Step-by-step explanation: Given Hyperbola equations :
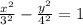 and
and
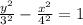
First one :
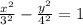 is a Horizontal Hyperbola.
is a Horizontal Hyperbola.
a = 3 and 2a = 6.
Length of transverse axis = 6.
And second one :
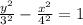 is a Vertical Hyperbola.
is a Vertical Hyperbola.
b=3 and 2b = 6
Length of transverse axis = 6.
The lengths of both transverse axes are the same.
Therefore, correct option is B option :
The lengths of both transverse axes are the same.