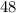let
x-------> the number of Lucy's orders
y-------> the number of Sam's orders
z-------> the number of Bob's orders
we know that
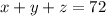 ----> equation A
----> equation A
 -----> equation B
-----> equation B
 -----> equation C
-----> equation C
substitute equation B and C in equation A
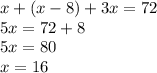
find z
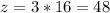
find y
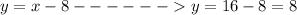
therefore
the answer is
the number of Lucy's orders is
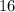
the number of Sam's orders is
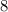
the number of Bob's orders is