Answer:
The graph in option (c) is the correct answer.
Explanation:
The line corresponding to the inequality
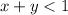 represents the dashed line and the line corresponding to the inequality
represents the dashed line and the line corresponding to the inequality
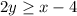 represents the solid line.
represents the solid line.
In order to figure out the correct shaded region, we test one point from each of the four possible regions and figure out the point at which both the inequalities bold true. The region containing that point would be the correct shaded region.
Let us test the point (0,0).
First inequality
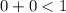 , that is,
, that is,
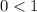 holds true.
holds true.
The second inequality
 that is,
that is,
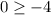 as well holds true.
as well holds true.
Since both the inequalities hold true at point (0,0), therefore, region containing origin is the correct answer. Thus, the correct answer is forth option. Since the options are not labeled, I have attached the correct graph with my solution in order to make sure you get the correct answer.