Question

Time (hours) Cost (dollars) 1 180 2 240 3 300 4 360 5 420 6 480 7 540 8 600 The table gives the cost for renting a limousine from Grey’s Limousine Rental. Which equation represents the company's fare structure, based on the amount of time it is rented? A. y = 60x B. y = 120x + 60 C. y = 60x + 120 D. y = 75x + 60

Answer 1

C

Explanation:

I took it and got it right

Answer 2

For this case we have:

By definition, two points are needed to find the equation of a line. We have a series of points given by:

`(x, y) = (time, cost)`

We chose two points:

`(t1, c1) = (1,180)\\(t2, c2) = (2,240)`

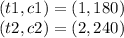
By definition, the formula of the slope is given by:

`m =((c2-c1))/((t2-t1))`

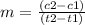
Substituting:

`m =(240-180)/(2-1)`

`m =(60)/(1)\\m = 60`

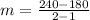
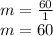
Being a line of the form
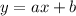`y = ax + b`, we substitute a point and the slope found to find the cut point b.

`180 = 60 * 1 + b\\180 = 60 + b\\b = 180-60\\b = 120`

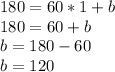
Thus, the equation of the line is given by:

`y = 60x + 120`

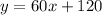
Answer:

Option C