For this case we have:
By definition, to find the slope of a line you need two points where the line passes.
Looking at the graph we can see that the line passes through the following points:
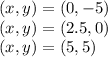
We chose two points:
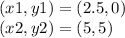
The equation of the slope is given by:
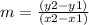
Substituting we have:
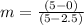
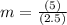
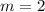
On the other hand, the linear equation of a line is given by:
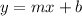
We substitute a point and the slope found to find the cut point b:
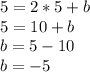
Thus, the equation of the line is given by:
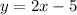
Answer:
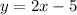
Option D