Question

Please Help It Is Past Due!

Prove the Pythagorean Theorem using similar triangles. The Pythagorean Theorem states that in a right triangle, the sum of the squares of the lengths of the legs of the triangle equals the squared length of the hypotenuse. Be sure to create and name the appropriate geometric figures.

Answer 1

Step-by-step explanation:

First we consider ΔABC and ΔBCD,

∠C=∠C (common)

∠B=∠D=
`90\textdegree`

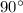
So, ΔABC ≈ ΔBCD (By AA similarity rule )

So by taking corresponding sides in ratios we get

`(AB)/(BD)=(AC)/(BC)=(BC)/(CD)`

Now

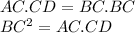`AC.CD=BC.BC\\BC^(2) =AC.CD` -------- Eqn (1)

Similarly,

We consider ΔABD and ΔABC

∠A=∠A (Commom)

∠B=∠D=
`90\textdegree`

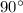
So,

ΔABD ≈ ΔABC (By AA similarity rule )

So by taking corresponding sides in ratios we get

`(BC)/(BD)=(AC)/(AB)=(AB)/(AD)`

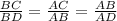
Now,

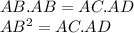`AB.AB=AC.AD\\AB^(2) =AC.AD` --------Eqn (2)

By Adding both the equation we get

`AB^2+BC^2=AC.CD+AC.AD\\AB^2+BC^2=AC(CD+AD)\\AB^2+BC^2=AC.AC\\AB^2+BC^2=AC^2`

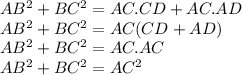
Hence, we proved the pythagorean theorem by using similarity of triangle.