Step-by-step explanation:
First we consider ΔABC and ΔBCD,
∠C=∠C (common)
∠B=∠D=
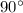
So, ΔABC ≈ ΔBCD (By AA similarity rule )
So by taking corresponding sides in ratios we get
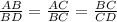
Now
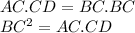 -------- Eqn (1)
-------- Eqn (1)
Similarly,
We consider ΔABD and ΔABC
∠A=∠A (Commom)
∠B=∠D=
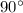
So,
ΔABD ≈ ΔABC (By AA similarity rule )
So by taking corresponding sides in ratios we get
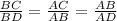
Now,
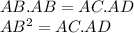 --------Eqn (2)
--------Eqn (2)
By Adding both the equation we get
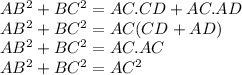
Hence, we proved the pythagorean theorem by using similarity of triangle.