For this case we have the following variables:
A: Represents the number of adults
S: Represents the number of students
C: Represents the number of children
For the income we have:
 -----> (1)
-----> (1)
Regarding the number of people at the concert we have:
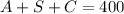 -----> (2)
-----> (2)
If there are 40 more children than students, we have:
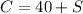 -----> (3)
-----> (3)
We substitute C in the second equation and it remains:
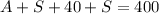


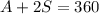
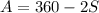 --------> (4)
--------> (4)
Substituting (3) and (4) in (1) we have:

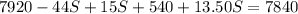
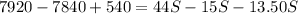
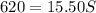
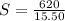

So, there are 40 children.
Substituting S in (3) and obtaining C:
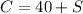

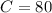
Substituting S in (4):
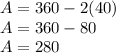
Thus, 280 tickets of adults, 80 of children and 40 of students were sold.
Answer:
280 tickets for adults, 80 for children and 40 for students