Question

Let f(x)= 3x+5 and g(x)=3x^2-x-10. Find (f/g)(x) and state its domain.

A. 2x-3; domain is the set of all real numbers
B. 1/x-2; domain is the set of all real numbers except 2
C. 3x+5; domain is the set of all real numbers
D. 2x+3/x-1; domain is the set of all real numbers except 1

Answer 1

Option: B is the correct answer.

The function is:
`((f)/(g))(x)=(1)/(x-2)`

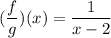
and the domain is: The set of all real numbers except 2

Explanation:

We are given a function f(x) and g(x) in terms of variable x by:

`f(x)=3x+5`

and

`g(x)=3x^2-x-10`

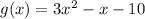
Now, the function

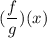`((f)/(g))(x)` is given by:

`((f)/(g))(x)=(f(x))/(g(x))`

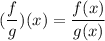
i.e.

`((f)/(g))(x)=(3x+5)/(3x^2-x-10)`

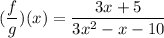
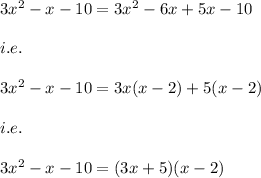
`3x^2-x-10=3x^2-6x+5x-10\\\\i.e.\\\\3x^2-x-10=3x(x-2)+5(x-2)\\\\i.e.\\\\3x^2-x-10=(3x+5)(x-2)`

i.e.

`((f)/(g))(x)=(3x+5)/((3x+5)(x-2))\\\\i.e.\\\\((f)/(g))(x)=(1)/(x-2)`

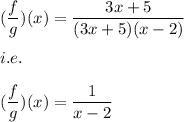
Also, the domain of the function is the set of all the real values except where the denominator is equal to zero.

The denominator is equal to zero when x=2.

Hence, the domain is the set of all the real values except 2.

Answer 2

Option B

Explanation:

Given that f(x) = 3x+5 and g(x) = 3x^2-x-10

Hence the function f/g = (3x+5)/(3x^2-x-10)

Since denominator cannot be 0 we have

3x^2-x-10 cannot be 0

i.e. x should not take values where 3x^2-x-10 =0

Solving (3x+5)(x-2) =0

x cannot take value as 2 or -5/3

So we can cancel 3x+5 and write

f/g =1/ x-2

Hence x cannot take values as 2

Option B