Answer:
The midpoint of AB is (0.5,1).
Explanation:
From the given graph it is clear that the vertices of the triangle ABC are A(-2,5), B(3,-3) and C(-4,-1).
If end points of a line segment are
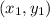 and
and
 , then the midpoint of that segment is
, then the midpoint of that segment is
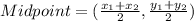
We need to find the midpoint of AB.
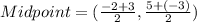

On further simplification we get
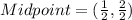

Therefore the midpoint of AB is (0.5,1).