Answer:
AB and CD are parallel to each other.
Explanation:
We have to check whether the line segment AB and CD are parallel, perpendicular or nothing,
The coordinates of A, B, C , D are:
A(2, 8), B(−1, −2), C(3, 7), D(0, −3)
We calculate the slope of line segment AB and CD.
Formula:

Putting the values, we get,
Slope of Line segment of AB =
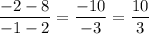
Slope of Line segment of CD =
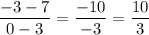
Thus,
Slope of Line segment of AB = Slope of Line segment of CD
Hence, the two line segments AB and CD are parallel to each other.