Question

Differentiate f(x)=x^2sin(x)

Answer 1

`\displaystyle \large{f\prime(x) = 2x \sin (x) + x^2 \cos (x)}`

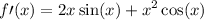
Explanation:

We are given a function:

`\displaystyle \large{f(x) = x^2 \sin (x)}`

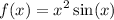
Notice that there are two functions multiplying each other. Recall the product rules.

`\displaystyle \large{y=h(x)g(x) \to y\prime = h\prime (x) g(x) + h(x)g\prime (x)}`

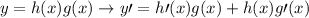
You can let x^2 = h(x), sin(x) = g(x) or sin(x) = h(x), x^2 = g(x) as your desire but I’ll let h(x) = x^2 and g(x) = sin(x).

Therefore, from a function:

`\displaystyle \large{f(x) = x^2 \sin (x) \to f\prime (x) = (x^2)\prime \sin(x) + x^2 (\sin (x))\prime}`

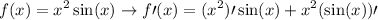
Recall the power rules and differentiation of sine.

`\displaystyle \large{y = ax^n \to y\prime = nax^(n-1) \ \ \ \tt{for \ \ polynomial \ \ function}}\\ \displaystyle \large{y = \sin (x) \to y\prime = \cos (x) }`

Therefore, from differentiating function,

`\displaystyle \large{f\prime(x) = 2x \sin (x) + x^2 \cos (x)}`

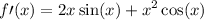
And we are done!