Question

What are the coordinates for the center of the circle and the length of the radius ?

Answer 1

the answer to your question is D

Answer 2

Answer: the correct option is

(D) (-7, -1), 6 units.

Step-by-step explanation: We are given to find the co-ordinates of the center and the length of the radius of the following circle :

`x^2+y^2+14x+2y+14=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

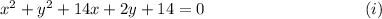
We know that

the STANDARD equation of a circle with center at the point (h, k) and radius of length r units is given by

`(x-h)^2+(y-k)^2=r^2.`

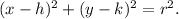
From equation (i), we have

`x^2+y^2+14x+2y+14=0\\\\\Rightarrow (x^2+14x+49)+(y^2+2y+1)+14-49-1=0\\\\\Rightarrow (x+7)^2+(y+1)^2-36=0\\\\\Rightarrow (x+7)^2+(y+1)^2=36\\\\\Rightarrow (x-(-7))^2+(y-(-1))^2=6^2.`

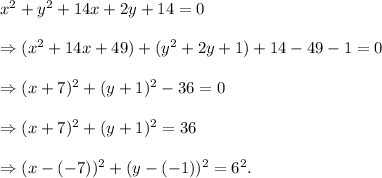
Comparing the above equation with the standard equation of a circle, we get

center, (h, k) = (-7, -1) and radius, r = 6 units.

Thus, (D) is the correct option.