Answer:
The coordinates of endpoint C are (7,-8).
Explanation:
Given information: Midpoint of BC is (5, -2) and B(3,4).
We need to find the coordinates of C.
Let the coordinate of C are (x,y).
If end points of a line segment are
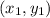 and
and
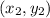 , then the midpoint of that segment is
, then the midpoint of that segment is
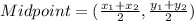
Midpoint of BC is
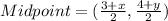
Midpoint of BC is (5,-2).
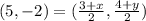
On comparing both sides.
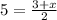
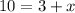
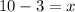
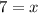
The value of x is 7.
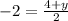
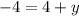
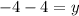
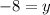
The value of y is -8.
Therefore the coordinates of endpoint C are (7,-8).