Question

The midpoint of BC is (5, -2). One endpoint is B (3,4). What are the coordinates of endpoint C?

Answer 1

Let the midpoint of
`BC` be
`M(x_(_M);~y_(_M))`.

Then
`x_(_M)=(x_(_B)+x_(_C))/(2)` and
`y_(_M)=(y_(_B)+y_(_C))/(2)`.

We are given
`x_(_M)=5, y_(_M)=-2` and
`x_(_B)=3, y_(_B)=4`.

`5=(3+x_(_C))/(2)\Rightarrow x_(_C)=7\medskip\\{-2}=(4+y_(_C))/(2)\Rightarrow y_(_C)=-8`

`C(7;-8)`

Answer 2

The coordinates of endpoint C are (7,-8).

Explanation:

Given information: Midpoint of BC is (5, -2) and B(3,4).

We need to find the coordinates of C.

Let the coordinate of C are (x,y).

If end points of a line segment are
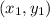`(x_1,y_1)` and
`(x_2,y_2)`, then the midpoint of that segment is

`Midpoint=((x_1+x_2)/(2),(y_1+y_2)/(2))`

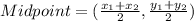
Midpoint of BC is

`Midpoint=((3+x)/(2),(4+y)/(2))`

Midpoint of BC is (5,-2).

`(5,-2)=((3+x)/(2),(4+y)/(2))`

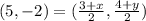
On comparing both sides.

`5=(3+x)/(2)`

`10=3+x`

`10-3=x`

`7=x`

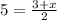
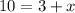
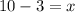
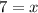
The value of x is 7.

`-2=(4+y)/(2)`

`-4=4+y`

`-4-4=y`

`-8=y`

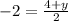
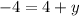
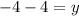
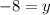
The value of y is -8.

Therefore the coordinates of endpoint C are (7,-8).