Question

How do I solve for x here? Use the properties of logarithms to find a value for x. Assume a,b, and M are constants.


`ln(a*b^(x)) = M`

The answer in the back of the textbook is
`x=(M-ln(a))/(ln(b))`

But I am unsure how to get to that solution. Do I start with ln(a) + ln(b)^x?

Answer 1

Yes, you're right! The first step is rewriting the equation as

`\ln(a) + \ln(b^x) = M`

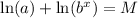
Subtract
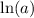`\ln(a)` from both sides:

`\ln(b^x) = M-\ln(a)`

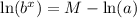
Use the property
`\ln(a^b) = b\ln(a)` to rewrite the equation as

`x\ln(b) = M-\ln(a)`

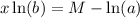
Divide both sides by
`\ln(b)`

`x = (M-\ln(a))/(\ln(b))`

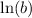
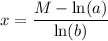
Alternative strategy:

Consider both sides as exponents of e:

`e^(\ln(ab^x)) = e^M`

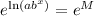
Use
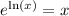`e^(\ln(x)) = x` to write

`ab^x = e^M`

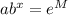
Divide both sides by a:

`b^x = (e^M)/(a)`

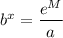
Consider the logarithm base b of both sides:

`x = \log_b\left((e^M)/(a)\right)`

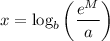
The two numbers are the same: you can check it using the rule for changing the base of logarithms