Question

A robot is exploring​ charon, the dwarf planet​ pluto's largest moon. Gravity on charon is 0.278 meters per second ​[m divided by s squared​]. During its​ investigations, the robot picks up a small spherical rock for inspection. The rock has a diameter of 6 centimeters​ [cm] and is lifted 15 centimeters​ [cm] above the surface. The specific gravity of the rock is 10.8. The mechanism lifting the rock is powered by a 10​-volt ​[v] power supply and draws 1.83 milliamperes​ [ma] of current. It requires 12 seconds​ [s] to perform this lifting task. What is the efficiency of the​ robot

Answer 1

In order to find the efficiency first we will find the Change in Potential energy of the small stone that robot picked up

First we will find the mass of the stone

As it is given that stone is spherical in shape so first we will find its volume

`V = (4)/(3)\pi r^3`

`V = (4)/(3)\pi *((0.06)/(2))^3`

`V = 1.13 * 10^(-4) m^3`

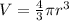
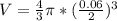
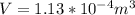
Now it is given that it's specific gravity is 10.8

So density of rock is

`\rho = 10.8 * 10^3 kg/m^3`

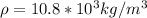
mass of the stone will be

`m = \rho V`

`m = 10.8* 10^3 * 1.13 * 10^(-4)`

`m = 1.22 kg`

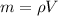
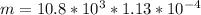
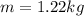
now change in potential energy is given as

`\Delta U = mgH`

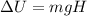
here

g = gravity on planet = 0.278 m/s^2

H = height lifted upwards = 15 cm

`\Delta U = 1.22* 0.278 * 0.15`

`\Delta U = 0.051 J`

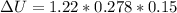
Now energy supplied by internal circuit of robot is given by

`E = Vit`

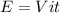
V = voltage supplied = 10 V

i = current = 1.83 mA

t = time = 12 s

`E = 10* 1.83 * 10^(-3) * 12`

`E = 0.22 J`

Now efficiency is defined as the ratio of output work with given amount of energy used

`\eta = (\Delta U)/(E)*100`

`\eta = (0.051)/(0.22) = 0.23`

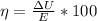
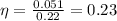
so efficiency will be 23 %