Question

Question 8

Solve the following system of equations using matrices.
3x – 2y = 31
3x + 2y = -1

(5, -8)

(3, 5)

(-3, 9)

(2, 8)

Answer 1

Solution is (5,-8)

3x – 2y = 31

3x + 2y = -1

first we write it in matrix form

3 -2 | 31 -------------> Row 1

3 2 | -1 -------------> Row 2

We use row operations and get matrix in 1 0 and 0 1 form

Subtract Row 2 by row 1. R2 -> R2 - R1. So R1 remains the same

3 -2 | 31 -------------> Row 1

0 4 | -32 -------------> Row 2

Divide row 1 by 3, R1-> R1/3. So R2 remains the same

1
`(-2)/(3)` |
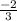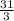`(31)/(3)` -------------> Row 1

0 4 | -32 -------------> Row 2

Divide row 2 by 4. R2 -> R2/4

1
`(-2)/(3)` |
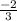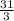`(31)/(3)` -------------> Row 1

0 1 | -8 -------------> Row 2

Now we need to get 0 in the place of -2/3

Multiply Row 2 by 2/3 and add it with Row 1. R1 --> 2/3 times R2 + R1

1
`1*(2)/(3)+(-2)/(3)` |
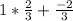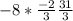`-8*(-2)/(3)(31)/(3)` -------------> Row 1

0 1 | -8 -------------> Row 2

Now simplify the fraction

1 0 | 5 -------------> Row 1

0 1 | -8 -------------> Row 2

So from this we can see that x=5 and y = -8

Solution is (5,-8)

Answer 2

we are given

system of equations

First equation is

`3x-2y=31`

Second equation is

`3x+2y=-1`

now, we can find augmented matrix

`A=\begin{pmatrix}3&-2&31\\ 3&2&-1\end{pmatrix}`

now, we can change it into reduced row echelon form

step-1: multiply the 1st row by 1/3

`A=\begin{pmatrix}1&-2/3&31/3\\ 3&2&-1\end{pmatrix}`

step-2:add -3 times the 1st row to the 2nd row

`A=\begin{pmatrix}1&-2/3&31/3\\ 0&4&-32\end{pmatrix}`

step-3:multiply the 2nd row by 1/4

`A=\begin{pmatrix}1&-2/3&31/3\\ 0&1&-8\end{pmatrix}`

step-4: add 2/3 times the 2nd row to the 1st row

`A=\begin{pmatrix}1&0&5\\ 0&1&-8\end{pmatrix}`

so, we get

`x=5,y=-8`

Answer is (5,-8)