Answer:
Stopping distance, s = 200 meters
Step-by-step explanation:
Mass of the car, m = 2000 kg
Force acting in the car, F = -2000 N
Initial speed of car, u = 20 m/s
Finally, it stops, v = 0
Using second equation of motion as :
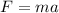
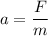
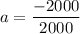
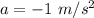
Let s is the stopping distance. Now using third equation of motion as :
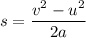
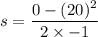
s = 200 meters
So, the stopping distance of the car is 200 meters. Hence, this is the required solution.